La règle de trois s'utilise notamment dans le calcul de pourcentages,  dans la résolution de problèmes de conversion d’unités, dans les problèmes de dosages, pour les recettes de cuisine, pour les calculs de moyennes de vitesse… et mille et une autres applications de la vie courante.

Pour que la guerre de la règle trois n'aie pas lieu, nous présentons deux méthodes. À chacun de choisir celle qu'il comprendra le mieux.

1. Méthode à l'ancienne: on ramène à l'unité puis on multiplie par le nombre désiré :

3,5Kg de viande coûtent 50€. Combien coûtent 6,2Kg de viande ?

Raisonnement à retenir : si 3,5Kg coûtent 50€, un Kilo coûtera 3,5 fois moins et 6,2Kg coûteront 6,2 fois plus.

On trace une barre et on pose, en haut à gauche la valeur de l'élément qu’on doit chercher (si on cherche des Euros, on pose la valeur Euros en haut à gauche).

50€
________________

On divise par le nombre de valeurs données (posé en bas) .

50€
________________
         3,5 Kilos
On multiplie par le nombre de valeurs demandées.

50 (€)   x   6,2 Kilos
________________ = 88,57€
        3,5 Kilos

--------------------

2. Méthode préconisée par les mathématiciens puristes (tout aussi efficace)

3,5Kg de viande coûtent 50€. Combien coûtent 6,2Kg de viande ?

1 – Faites un schéma explicatif (si possible en dessinant un tableau)

Ligne 1 : 3.5Kg coûtent 50€
Ligne 2 : ce que vous devez calculer 6.2Kg et le point d'interrogation représente le résultat à obtenir.

Ensuite faites votre tracé : il commence en diagonale par celle où il y a les deux chiffre et non le ?

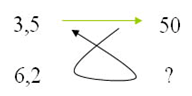
3 – Appliquez la méthode ci dessous :
Pour obtenir le résultat, il faut multiplier les deux chiffres qui sont dans la diagonale où ils sont présents et diviser le résultat de la multiplication par le chiffre qui reste.
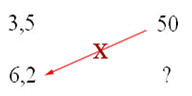et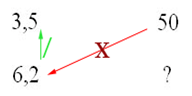
6.2Kg x 50€ / 3.5Kg = 88.57€... ce qui revient au même mais on a commencé par la multiplication !!!

----------------------

Exemple : J'ai consommé 9 litres d'essence pour parcourir 153Km. Combien dois-je prévoir de litres d'essence pour 600Km?

méthode N°1

- Commencez le raisonnement par l’élément à calculer (nombre de litres d'essence: 9)
- Si 9litres d'essence permettent de parcourir 155Km, pour 1Km, je consommerai 9/155 et, pour 600Km, j'en consommerai 600 fois plus.

Pour vous faciliter la tâche, vous pouvez écrire :

9 (l)   x   600 (Km)
________________ = 36litres
      155 Km

----------------------

 

méthode N°2

9 ---------> 600
155             ?

 

soit : 9 x 600 /155 = 36 litres

 

--------------------

Essayez maintenant par l'une ou l'autre méthode :

On dispose d’un plan dont l’échelle indique que 2 cm sur la carte représentent 15 km sur le terrain. On sait que, sur la carte, la distance entre deux villes est de 12,2 cm. On cherche à déterminer la distance à vol d'oiseau entre ces deux villes.

Résultat à trouver : 91,5Km

-------------

Dans une recette de cuisine, il faut 600g de farine pour 4 personnes. Combien de farine faudra-t-il pour 7 personnes ?

Résultat à trouver : 1050g

 

 

1. Commencez le raisonnement par l’élément à calculer  (combien ? => la distance en Km => 15Km

    2. Ramenez-le à l’unité par une division 15Km : 2cm = 7,5 Km

    3. Multipliez-le par la quantité demandée. 7,5Km x 12,2  cm = 93.75Km

  
 

1. Commencez le raisonnement par l’élément à calculer (combien ?) =>  la quantité de farine => 600g

    2. Ramenez-le à l’unité par une division 600g : 4personnes = 150g

    3.  Multipliez-le par la quantité demandée. 150g x 7 personnes = 1050g de farine
  

  
 

divisez
  

  
 

multipliez